Bienvenue en orbite autour de l’option spécifique mathématiques et physique au Mont-sur-Lausanne.
En raison de la crise sanitaire, ce site accueille temporairement des informations liées aux cours de mathématiques de la 9VP1.
OSMEP9 – Objectif Terre, Objectif Lune, Voyage dans le système solaire
Eureka 9S – Chapitres d’ASTRONOMIE
Coup de pouce: 9S_Eureka_Coup_de_pouce_ASTRO
Livre: 9S_Eureka_Livre_ASTRO
Fichier: 9S_Eureka_Fichier_ASTRO
Corrigé: 9S_Eureka_corrige_ASTRO
Evaluation du 10 février 2022 – Objectif Terre
- Etre capable d’expliquer des phénomènes liés à la Terre: les saisons, la durée du jour et de la nuit.
- Etre capable d’expliquer à quoi correspondent l’équateur, les tropiques, les cercles polaires, les méridiens, les parallèles, les fuseaux horaires, les coordonnées géographiques d’un lieu.
- Etre capable de déterminer la circonférence d’un cercle dont on connaît le rayon (ficelle et calculs de proportionnalité ou formule du périmètre du cercle)
- Etre capable de calculer la vitesse de rotation et la vitesse de révolution d’un astre.
- Etre capable de résoudre des problèmes comme AS23, 24, 25, 27, 29, 30
OSMEP9 – Numérations
Eureka 9S – Chapitre Codes et congruence
Coup de pouce: 9S_Eureka_coup_de_pouce_CO
Livre: 9S_Eureka_Livre_CO
Fichier: 9S_Eureka_corrige_CO
Corrigé: 9S_Eureka_Fichier_CO
MATH9VP1 – Géométrie plane
Janvier 2022:
Dossier de révision à compléter à l’aide de l’aide-mémoire:
Aide-mémoire:
Corrigés ES et GM du livre et du fichier MATH9S:
Corrigés GM – Lignes et surfaces
MATH9VP1 – Nombres rationnels
Janvier 2022:
Plan de travail concernant les fractions:
LES FRACTIONS – Les nombres rationnels 9VP1
Corrigés des exercices complémentaires sur le plan de travail:
LES FRACTIONS – Les nombres rationnels 9VP1 corrige
Corrigés des exercices du livre et du fichier de math9S:
Corrigés NO-nombres rationnels
Voici quelques vidéos pour t’aider:
Mettre deux fractions au même dénominateur:
Encadrer une fraction par deux entiers consécutifs:
Modifier l’écriture d’une fraction:
Additions et soustractions de fractions:
OSMEP 11S: Valeur refuge, le rouleau de papier de toilette
Une valeur refuge, le rouleau de papier de toilette
But: Détermine la surface de papier de toilette dans un rouleau en utilisant la technique de Gauss pour calculer la somme d’une suite de termes (Eurêka 10S p.89).
Le papier s’enroule en spirale autour d’un cylindre central en carton. Nous pouvons faire l’approximation que la longueur de cette spirale correspond à la somme des périmètres de cercles concentriques de rayon R1, R2, R3, R4, …, Rn
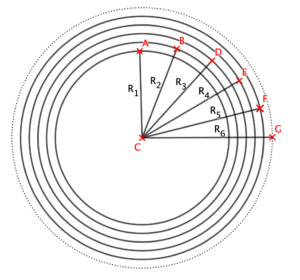
On constate que R2 – R1 = R3 – R2 = … = l’épaisseur d’une feuille de papier toilette
R1 correspond au rayon extérieur du cylindre central en carton
Rn correspond au rayon extérieur du rouleau de papier de toilette
Ne te reste plus qu’à prendre les mesures nécessaire sur un rouleau de papier de toilette et à effectuer quelques calculs pour trouver la surface de papier souhaitée.
Tu ne sais pas comment démarrer… regarde la vidéo au bas de cette page.
Si tu n’as pas de rouleau de papier de toilette, relève les mesures sur ces images :
40 feuilles sont superposées sur cette image:
MATHEMATICORIGOLO: Qui a mangé la tarte aux pommes?
Les quatre enfants de la famille Belledent ont tous eu un dessert différent aujourd’hui.
- Aline et les deux jumeaux n’ont pas voulu de glace aux fraises.
- Betty a trempé le doigt dans le flan au caramel de sa soeur. César, le petit dernier, a trouvé ça rigolo.
- Un des garçons a renversé une partie de sa crème au chocolat en se disputant avec son frère.
Qui a mangé la tarte aux pommes?
OSMEP 10S : Descente de nombres
Youpi, c’est mardi, enfin un nouveau problème de Fonctions!
Télécharger le chapitre Fonctions d’Eurêka 10S ici: FO_eurêka 10S
L’observation attentive de la manière dont a été créée cette pyramide de nombres te permettra de répondre aux questions:
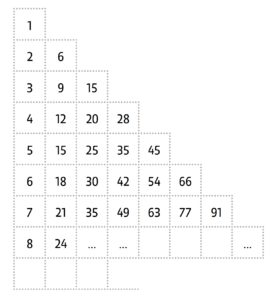
a. Quel est le dernier nombre de la 24ème ligne?
b. Quel est le dernier nombre de la nème ligne?
c. Quelle est la somme des nombres de la 24ème ligne?
d. Quelle est la somme des nombres de la nème ligne?
e. Quel est le nombre qui se trouve au milieu de la 111ème ligne?
Essaie de résoudre cette activité sans aide. Si tu n’y arrives pas, dans un premier temps, visionne une des vidéos ci-dessous et si tu as toujours un souci, envoie un mail à sandraprodhom@gmail.com
Une problème avec le point a. ? Visionne cette vidéo:
Une problème avec le point c. ? Visionne cette vidéo:
Une problème avec le point e. ? Visionne cette vidéo:
MATHEMATICORIGOLO: Valeur refuge, le rouleau de papier de toilette
Chacun a bien un rouleau de papier de toilette à domicile…
Et bien, sans le dérouler, hormis une dizaine de feuilles maximum, détermine quelle surface de papier de toilette un rouleau représente-t-il?
Pour t’aider ou si la balance de la cuisine est monopolisée par ton petit frère qui fait une délicieuse recette de cookies… Tu peux visionner ceci:
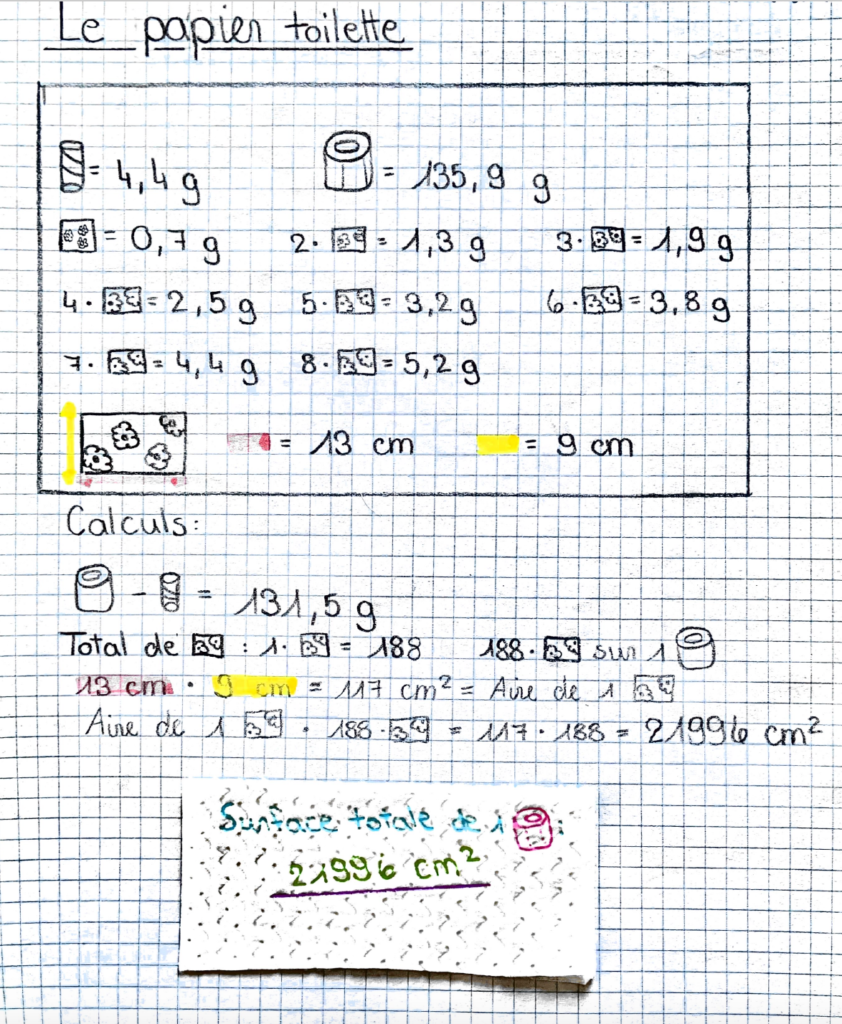
Voici le compte-rendu de Mathilde:
MATHEMATICORIGOLO: Magie, magie
Et si on préparait un petit tour de magie pour impressionner sa famille…
Visionne la vidéo suivante qui montre le tour de magie, enfin de « médiumnité », enfin disons plutôt de raisonnement déductif:
Comment savoir qui a le trésor?
Pour celles et ceux qui ont besoin d’un coup de pouce!
Voici la solution de Benoît:
Et le corrigé: tresor_corrigé
MATHEMATICORIGOLO: Ballet mathématique
Quand les math dansent…
Visionne cette vidéo
sources: @educlasse.ch
- Détermine la longueur du segment vert sachant que le segment noir mesure 1000 mm.
- Détermine la longueur du segment rouge.
- Détermine la longueur du segment bleu.
- En poursuivant la danse… Quel est le nom de la figure géométrique obtenue?
- Divise la mesure rouge par la bleue et fais quelques recherches sur le nombre obtenu.
Voici quelques solutions, celle de Benoît, celle de Anaïs:
Visionne cette vidéo pour en savoir plus sur le nombre d’or:
MATHEMATICORIGOLO: Compter comme les shadoks
Visionne cette vidéo et apprends à compter comme les shadoks.
Et voyons voir si tu as bien compris…
- Combien de shadoks peut-on mettre dans une poubelle? une grande poubelle? une super poubelle? une mega poubelle?
- A quel nombre correspond BuZoGaMeu?
- Comment se dit et s’écrit dans le nouveau langage mathématique des shadoks le nombre 2020?
- Regarde la vidéo Shadoks.mp4 ci-dessous qui te donnera quelques éléments de réponse.
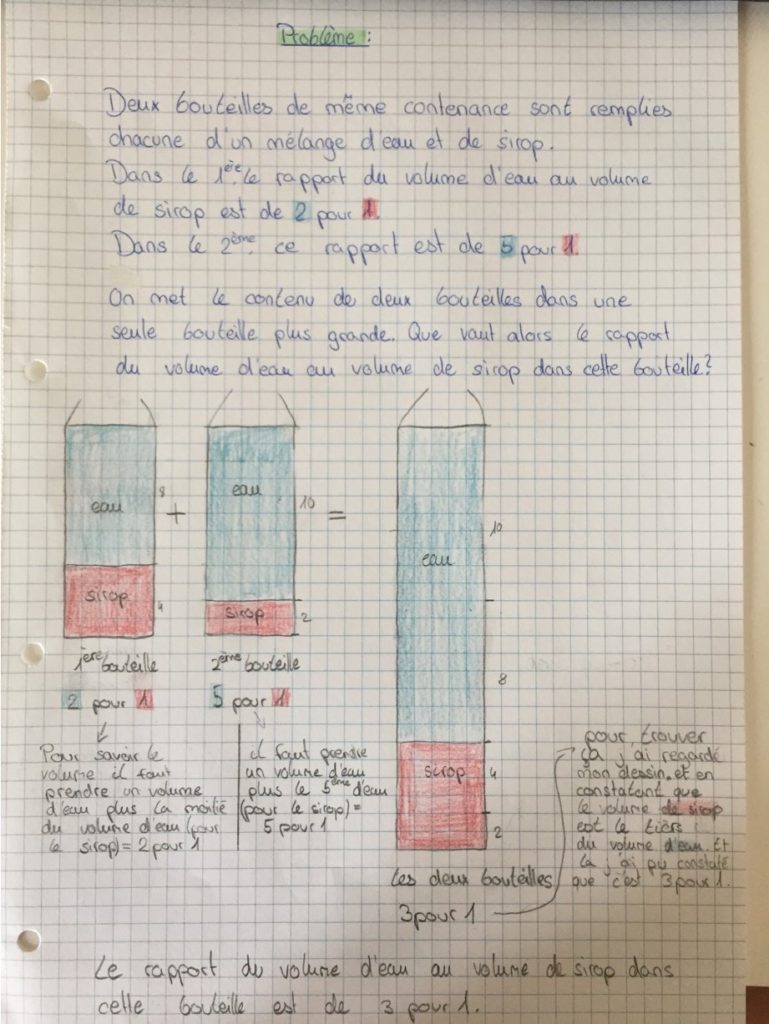
Voici la solution d’Arthur:
MATHEMATICORIGOLO: On se fait un sirop?
Avant de nous remettre tranquillement au travail, je vous propose de nous préparer un sirop.
Deux bouteilles de même contenance sont remplies chacune d’un mélange d’eau et de sirop.
Dans la première, le rapport du volume d’eau au volume de sirop est
de 2 pour 1.
Dans la seconde, le rapport est de 5 pour 1.
On met le contenu des deux bouteilles dans une seule bouteille plus grande.
Que vaut alors le rapport du volume d’eau au volume de sirop dans cette bouteille?
Voici la solution de Anna:
OSMEP 10S: Qui suis-je?
Un petit défi pour vous tous…
Qui suis-je?
Le produit du jour, du mois et de l’année de ma naissance est égal à 213’240.
Je suis né dans une ville au nord de l’Allemagne, commençant par la lettre B.
J’ai trouvé la position de Cérès en décembre.
Je sais construire certains polygones réguliers sans rapporteur.
J’ai fait des mathématiques, de la physique et de l’astronomie en particulier, mes spécialités!
La solution?
On va utiliser une de ses techniques pour calculer une somme de termes dès la semaine prochaine.
Carl Friedrich Gauss (1777 – 1855)
mathématicien, physicien et astronome allemand,
surnommé « Le prince des mathématiciens »
OSMEP 10S: Etude de fonctions
Visionne la vidéo suivante:
https://www.scolcast.ch/episode/eureka-10s-introduction-la-recherche-de-fonctions
Détermine la somme de n termes de S = 7+ 12 + 17 + 22 + …
Détermine la somme des termes compris entre 7 et N de S = 7+ 12 + 17 + 22 +…
Le chapitre d’Eurêka 10S sur les fonctions se télécharge ici: FO_eurêka 10S
Entraîne-toi en résolvant l’activité FO 40 et visionne l’aide pour FO 40 si nécessaire.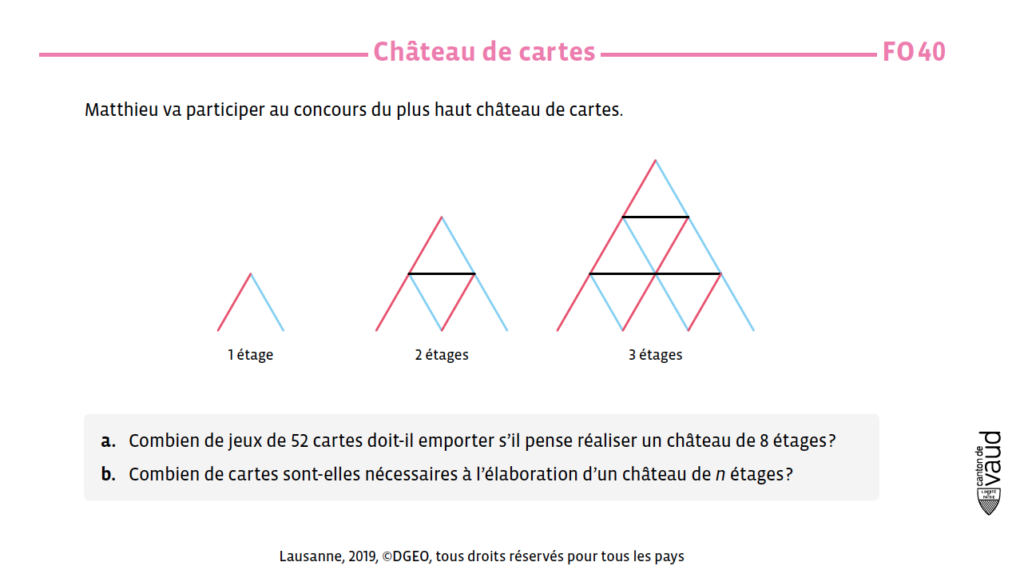
Voici une vidéo pour t’aider à démarrer FO 40:
Voici la solution de Loghan et Basile à propos de la somme 7 + 12 + 17 + 22 + …
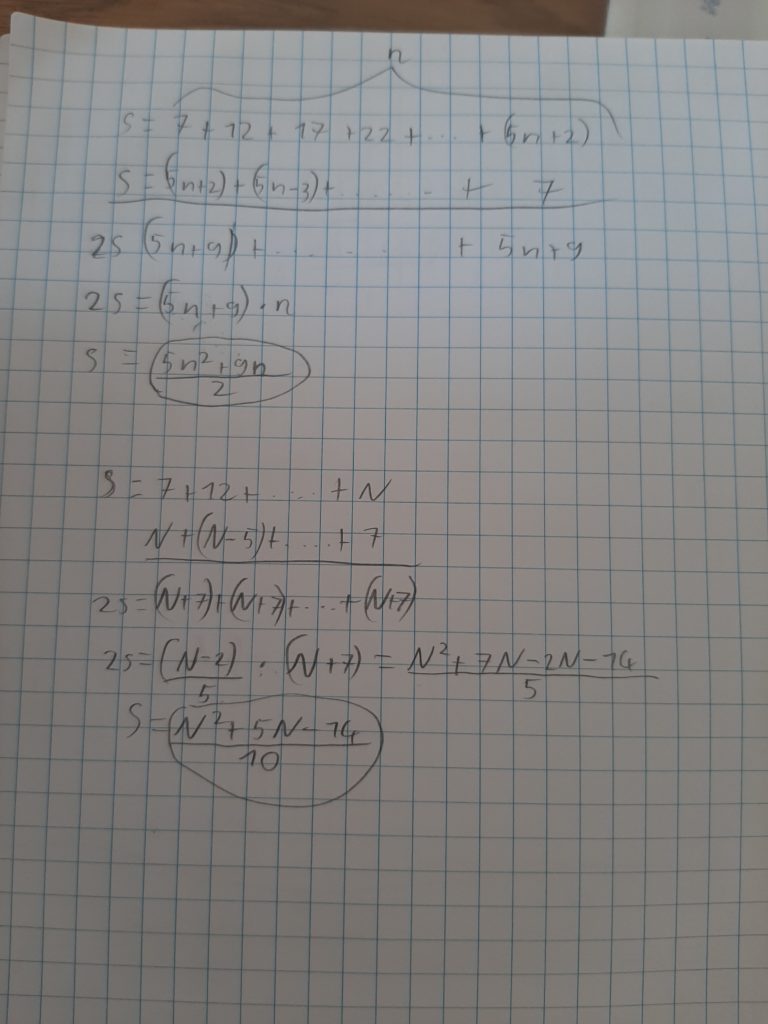
Voici le corrigé de FO 40:
OSMEP 11S: LG10 – Combinaison de doubles arcs capables
Un petit lieu géométrique pour bien commencé la journée
Des explications?
(https://www.scolcast.ch/episode/eureka-11s-lg-10)
Voici deux résolutions, celle de Nelia sur papier et celle de Tanguy sur GeoGebra (voir zone verte):
Le lieu géométrique est la zone verte. Les arcs capables constituant le bord de la zone appartiennent au lieu, mais les points B et C n’appartiennent pas au lieu.
OSMEP 11S: Prolongement de LG14 avec … un peu de calcul littéral
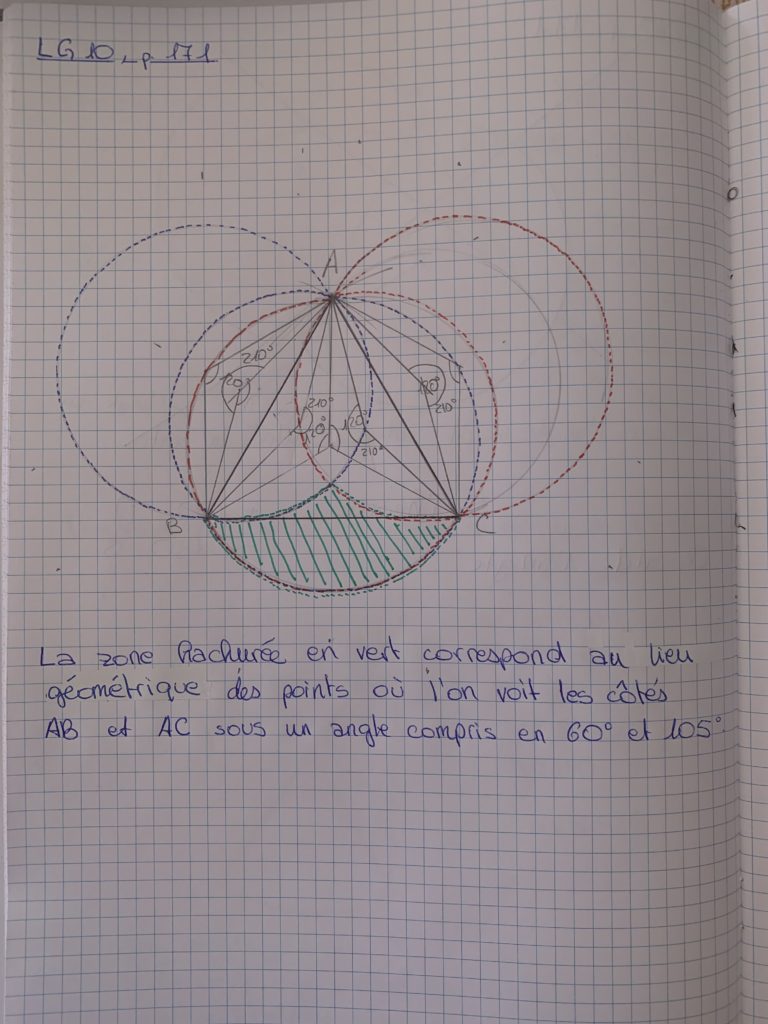
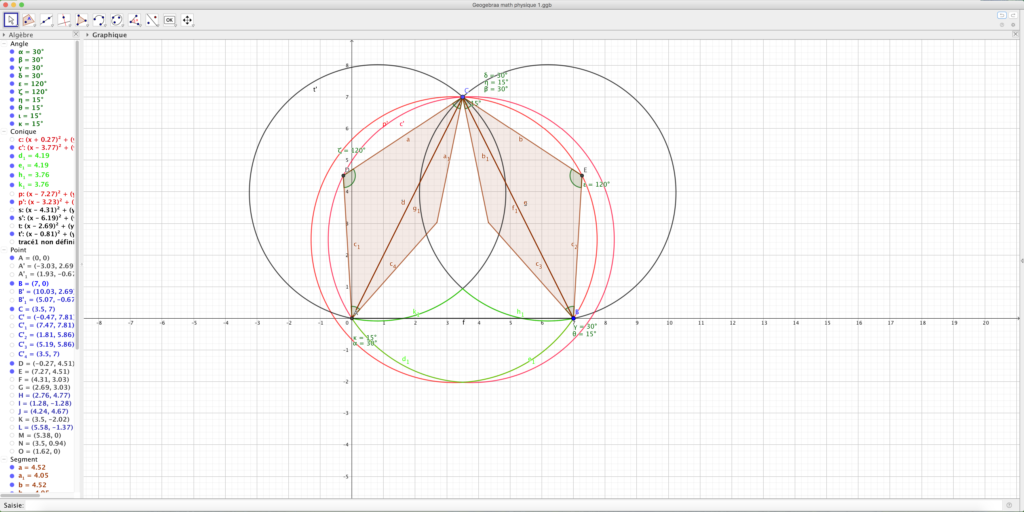
Good morning everybody,
On pose comme coordonnées pour A (0;0) et pour B (d;0).
On souhaite trouver le lieu géométrique des points n fois plus près de A que de B. Cherche en fonction de d et de n:
1) Soit P le point sur la circonférence du cercle entre A et B, quelles sont ses coordonnées?
2) Soit P’ le point sur la circonférence du cercle à gauche de A, quelles sont ses coordonnées?
3) Quelle est la mesure de la distance PP’? (diamètre du cercle)
4) Quelle est la mesure du rayon du cercle?
5) Quelles sont les coordonnées du centre du cercle?
Voici une petite vidéo qui vous donnera quelques clés pour résoudre le prolongement de LG14.
Essayez!
Voici la solution de Chloé pour le point 5):
OSMEP 11S : LG13 – Piraterie
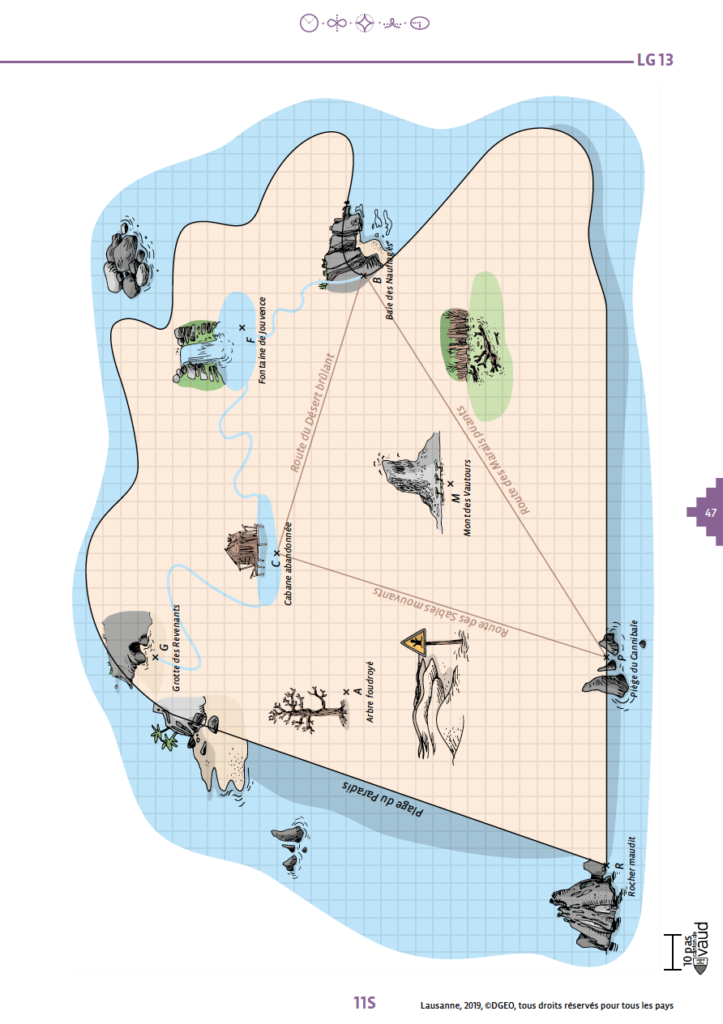
Tente de trouver un maximum de trésors cachés par neuf pirates. Pour cela, tu peux résoudre l’activité LG13 directement sur GeoGebra.
Chaque pirate a son propre document ggb. Tu peux télécharger ces neuf documents ci-dessous.
Pour vérifier l’emplacement d’un trésor, fais glisser le point bleu avec les initiales du pirate sur le lieu trouvé et vérifie son emplacement en appuyant sur le bouton « vérifier » ; un smiley vert indique que tu as trouvé l’emplacement correct du trésor. Trop cool, non?
Si tu n’arrives pas à te connecter à GeoGebra, tu peux travailler sur la fiche LG13.
Quelques trucs pour utiliser un curseur sur GeoGebra sont montrés dans cette vidéo: https://www.scolcast.ch/episode/geogebra-curseurs
Voici les fichiers GeoGebra à télécharger:
11_LG13_AE.ggb Pense à utiliser un curseur
11_LG13_RT.ggb Pense à la réflexion de la lumière
11_LG13_SB.ggb Pense à utiliser un curseur
Voici le corrigé pour celles et ceux qui ont travaillé sur feuille:
OSMEP 11S: TP Puissance et rendement
Le but de ce travail pratique est de déteminer la puissance électrique, la puissance thermique du thermoplongeur, ainsi que le rendement de ce système de chauffage.
Revois la théorie à propos de la puissance et du rendement dans Eurêka 11S p.211 et p.212
Visionne la vidéo de l’expérience https://www.scolcast.ch/episode/tp-puissance-et-rendement-dun-thermoplongeur et note les mesures qui te sont nécessaires pour atteindre le but de ce TP.
Rédige le principe général de l’expérience:
Décris l’idée globale de l’expérience, comment on se propose d’atteindre le but fixé.
Organise dans un tableau, l’ensemble des mesures nécessaires pour ce TP. N’oublie pas les unités.
Rédige le principe de la mesure:
Décris les mesures qui vont être effectuées. Explique les équations utilisées menant à la grandeur cherchée. N’oublie pas les unités.
Besoin d’un coup de pouce? Visionne cette vidéo.
OSMEP 11S: TP Chaleur latente de vaporisation de l’eau
Le but de ce travail pratique est de déterminer la chaleur latente de vaporisation de l’eau.
Les résultats obtenus pour le TP Puissance du thermoplongeur et rendement d’un système de chauffage te seront nécessaires pour mener à bien ce TP.
Revois la théorie à propos de l’énergie thermique dans Eurêka 11S p.202 et à propos des changements d’états dans Eurêka 11S p. 209 et 210.
Visionne la vidéo de l’expérience
(https://www.scolcast.ch/episode/tp-chaleur-latente-de-vaporisation-de-leau)
et note les mesures qui te sont nécessaires pour atteindre le but de ce TP.
Rédige le principe général de l’expérience:
Décris l’idée globale de l’expérience, comment on se propose d’atteindre le but fixé.
Organise dans un tableau, l’ensemble des mesures nécessaires pour ce TP. N’oublie pas les unités.
Rédige le principe de la mesure:
Décris les mesures qui vont être effectuées. Explique les équations utilisées menant à la grandeur cherchée. N’oublie pas les unités.
Compare ton résultat avec la valeur théorique Lv = 23 · 10^5 J/kg et indique précisément au moins un élément justifiant la différence.
Besoin d’un coup de pouce? Visionne cette vidéo.
La minute scientifique
Antenne branchée sur Radiobus!
Les élèves d’option spécifique mathématiques et physique 9S ont réalisé des capsules scientifiques d’une minute et quelques.
Bonne écoute.
Le moteur asthmatique
A présent, une petite minute scientifique avec Arthur et Sébastian qui vont vous expliquer pourquoi le moteur d’une voiture cale plus facilement en altitude.
Big Splat ou la formation de la Lune
Benoît et Kevin vous emmène il y a 4,5 milliards d’année lors de la formation de la Lune. Embarquez dans la fusée Apollo, ça commence !
Passons le mur du son
Prêts pour le grand Bang ? Marie et Ilhan vont nous faire franchir le mur du son.
A la découverte des trous noirs
A présent, une petite minute scientifique avec Daniel et Ethan qui vont vous expliquer le concept de ce qu’est un trou noir, attachez vos ceintures, accrochez-vous à la gravité ou vous serez aspirés !
La plus grande supernova
Pascal et Loghan vont vous présenter la plus grande supernova. Prêts au décollage ?
Bleu, le ciel est bleu. Mais pourquoi ?
Timothée et Sam vont vous emmener à la mer, euh non plutôt ils vont vous expliquer pourquoi la mer et le ciel sont bleus.
Ca gaze avec les boissons gazeuses
Pourquoi entend-on un petit psss lorsqu’on secoue et ouvre une bouteille de soda ?
Nahel et Luka vous diront le pourquoi et le comment de ce petit bruit qui désaltère.
Chaud-froid
Ardian, Maxime et Ludovic vont vous expliquer pourquoi l’azote liquide est plus froid que le fer liquide. Mettez un bonnet, la température va descendre à -200°C.
Vous saurez tout sur la foudre
Vous aurez le coup de foudre pour la chronique de Melvyn et Julien. Ca tombe bien, ils vont vous parler de la foudre !
Oumuamua, késako ?
Léna, Nadia et Cécile pensent que les aliens nous ont trouvés ! La preuve ? Ecoutez leur chronique scientifique.
Et si la Lune disparaissait ?
La Lune s’éloigne de 4 cm chaque année. Et si la Lune nous quittait ! Basile et Erjon vous disent tout sur les conséquences d’une telle disparition.
Boum !
Arno et Matteo vont vous parler de la bombe atomique qui a détruit la ville japonaise de Hiroshima, ce qui a mis fin à la deuxième guerre mondiale.